Diferența dintre paralelogramă și rhombus: paralelogramă vs rhombus

Parallelogram vs Rhombus

romburile sunt patrulaterale. Geometria acestor figuri a fost cunoscută omului de mii de ani. Subiectul este tratat în mod explicit în cartea "Elemente", scrisă de matematicianul grec Euclid.

Paralelogramă

Paralelogramul poate fi definit ca figură geometrică cu patru laturi, cu laturi opuse paralele unul cu celălalt. Mai exact, este un patrulater cu două perechi de laturi paralele. Această natură paralelă oferă numeroase caracteristici geometrice paralelogramelor.

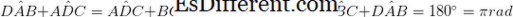
Un quadrilateral este un paralelogram dacă se găsesc următoarele caracteristici geometrice.

• Două perechi de laturi opuse sunt egale în lungime. (AB = DC, AD = BC)

• Două perechi de unghiuri opuse sunt egale în mărime. (

)

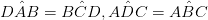
• Dacă unghiurile adiacente sunt suplimentare

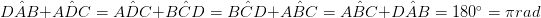
• O pereche de laturi, care se opun reciproc, este paralelă și egală în lungime. (AB = DC & AB *)

• Diagonalele se intersectează reciproc (AO = OC, BO = OD)

• Fiecare diagonală împarte patrulaterul în două triunghiuri congruente. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

În plus, suma pătratelor laturilor este egală cu suma pătratelor de diagonale. Aceasta este uneori menționată drept legea paralelogramă și are aplicații pe scară largă în fizică și inginerie. (² + BC ² + CD ² 2 ⁾ Fiecare dintre caracteristicile de mai sus poate fi utilizată ca proprietăți, odată ce se stabilește că tetraarila este o paralelă. ^{Suprafața paralelogramului poate fi calculată de produsul dintre lungimea unei laturi și înălțimea față de partea opusă. Prin urmare, aria paralelogramului poate fi declarată ca fiind} Aria paralelogramului = baza × înălțimea = AB × h ^{Suprafața paralelogramului este independentă de forma paralelogramului individual. Este dependentă numai de lungimea bazei și de înălțimea perpendiculară.} Dacă părțile laterale ale unei paralelaograme pot fi reprezentate de doi vectori, zona poate fi obținută prin magnitudinea produsului vectorial (produsul încrucișat) al celor doi vectori adiacenți.

Dacă părțile AB și AD sunt reprezentate de vectori () și respectiv, zona paralelogramului este dată de

, unde α este unghiul

și.

Următoarele sunt proprietățile avansate ale paralelogramului;

• Zona paralelogramului este de două ori aria unui triunghi creat de oricare dintre diagonalele sale.

• Suprafața paralelogramului este împărțită pe jumătate de orice linie care trece prin punctul central.

• Orice transformare afină non-degenerată face paralelogramă cu un alt paralelogram

• Paralelogramul are simetrie rotativă de ordine 2

• Suma distanțelor față de orice interior al paralelogramului față de laturi este independentă de locația punctului

Rhombus

Un patrulater cu toate laturile sunt egale în lungime este cunoscut ca un romb. Este, de asemenea, numit ca

patrulaterală echilaterală

. Se consideră că are o formă de diamant, similar cu cea din cărțile de joc.

Rhombus este, de asemenea, un caz special al paralelogramului. Acesta poate fi considerat drept paralelogram cu toate cele patru laturi egale. Și are proprietăți speciale, în plus față de proprietățile unei paralelograme.

• Diagonalele rombului se intersectează unghi drept; diagonalele sunt perpendiculare.

• Diagonalele bisectează cele două unghiuri opuse.

• Cel puțin două dintre laturile adiacente sunt egale în lungime. Suprafața rombului poate fi calculată în aceeași metodă cu cea a paralelogramului. Care este diferența dintre Parallelogram și Rhombus?

• Paralelogramul și rombiul sunt patrulaterale. Rhombus este un caz special al paralogului.

• Suprafața oricărui domeniu poate fi calculată folosind formula de bază × înălțime.

• Considerând diagonalele;

- diagonalele paralelogramului se intersectează reciproc și bisect paralelograma pentru a forma două triunghiuri congruente.

- Diagonalele rombului se intersectează unghi drept, iar triunghiurile formate sunt echilaterale.

• Luând în considerare unghiurile interne;

- Unghiurile interioare opuse ale paralelogramului sunt egale în mărime. Două unghiuri adiacente interne sunt suplimentare.

Unghiurile interne ale rombului sunt divizate de diagonale.

• Având în vedere părțile laterale;

- În paralelogramă, suma pătratelor laturilor este egală cu suma pătratelor diagonale (Legea paralelogramelor).

- Întrucât toate cele patru laturi sunt egale într-un romb, de patru ori pătratul unei părți este egal cu suma pătratelor diagonale.