Diferența dintre derivatul și diferențialul

Derivat vs. Diferențial

În calculul diferențial, derivatele și diferențele unei funcții sunt strâns legate, dar au semnificații foarte diferite și utilizate pentru a reprezenta două obiecte matematice importante legate de funcții diferențiate.

Ce este derivat?

Derivatul unei funcții măsoară rata la care valoarea funcției se modifică odată cu modificarea intrării acesteia. În funcțiile cu mai multe variabile, modificarea valorii funcției depinde de direcția schimbării valorilor variabilelor independente. Prin urmare, în astfel de cazuri, este aleasă o anumită direcție și funcția este diferențiată în direcția respectivă. Acest derivat se numește derivat direcțional. Derivații parțiali reprezintă un tip special de derivate direcționale.

Derivația unei funcții cu valoare vectorială f poate fi definită ca limita

oriunde există finit. Așa cum am menționat mai sus, aceasta ne dă rata de creștere a funcției f de-a lungul direcției vectorului u. În cazul unei funcții cu valoare unică, aceasta se reduce la definiția binecunoscută a derivatului,

-

De exemplu,

este peste tot diferențiabil, iar derivatul este egal cu limita,

, care este egală cu

. Derivații de funcții precum

există peste tot. Acestea sunt egale cu funcțiile

.

Acesta este cunoscut ca primul derivat. De obicei, primul derivat al funcției f este notat cu f ⁽¹⁾ . Acum, folosind această notație, este posibil să se definească derivate de ordin superior.

este derivatul direcțional de ordinul doi și denotând derivatul n cu f ^{(n n} ,, definește derivatul n

. ^{Ce este diferențialul?} Diferența unei funcții reprezintă modificarea funcției în funcție de variațiile variabilei sau variabilelor independente. În notația obișnuită, pentru o funcție dată

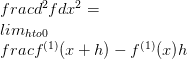
f

a unei singure variabile x, diferența totală a ordinului 1 df este dată de. Aceasta înseamnă că pentru o schimbare infinitezimală în x

(adică d x), va fi f (1)) d ^x schimbare în f. Utilizarea limitelor se poate face cu această definiție după cum urmează. Să presupunem că x este schimbarea în x

la un punct arbitrar x și Δ f. Se poate arăta că Δ f = f (1) (x) Δ x + ^ε eroarea. Acum, limita Δ x 0 Δ > x) (folosind definiția definită anterior a derivatului) și astfel, Δ ^{x → 0} ε _{> = 0.Prin urmare, se poate concluziona că, Δ x →} 0 ε ^{= 0. Acum denotând Δ} x → ca d f și Δ x → 0 Δ ^x ca d _{x definiția diferențialului este obținută riguros.} De exemplu, diferența funcției este. În cazul funcțiilor a două sau mai multe variabile, diferența totală a unei funcții este definită ca suma diferențialelor în direcțiile fiecărei variabile independente. Din punct de vedere matematic, poate fi declarat. Care este diferența dintre derivat și diferențial? • Derivatul se referă la o rată de schimbare a unei funcții, în timp ce diferența se referă la schimbarea reală a funcției, atunci când variabila independentă este supusă schimbării. • Derivatul este dat de, dar diferența este dată de.