Diferența dintre integrali definiți și nedefiniți Diferența dintre

Calculul este o ramură importantă a matematicii, iar diferențierea joacă un rol critic în calcul. Procesul invers al diferențierii este cunoscut sub numele de integrare, iar inversul este cunoscut ca integrarea, sau pur și simplu pus, inversul diferențierii dă un integru. Pe baza rezultatelor pe care le produc integralele sunt împărțite în două clase viz., integrale definite și nedefinite.

Definit Integral

(999) f (x)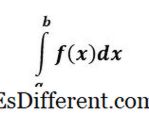

este un NUMBER și reprezintă aria de sub curbă f (x) de la x = a la x = b . Un integral integrat are limite superioare și inferioare ale integralelor și se numește definitiv deoarece, la sfârșitul problemei, avem un număr - este un răspuns clar. - Integrala indefinita

Integralul indefinit al lui f (x) este o FUNCTIE si raspunde la intrebarea "Ce functie atunci cand diferentiata da

f (x)

? "

Cu un integrat indefinit nu există limite superioare și inferioare ale integralității aici și ceea ce vom obține este un răspuns care încă are x în el și va avea, de asemenea, o constantă (denumită de obicei cu

C ).

Integralul indefinit oferă de obicei o soluție generală la ecuația diferențială. Integralul indefinit este mai mult o formă generală de integrare și poate fi interpretat ca fiind un derivat al funcției considerate.

Să presupunem că diferențierea funcției

F

duce la o altă funcție

f , iar integrarea lui f dă integritatea. În mod simbolic, aceasta este scrisă ca F (x) = ∫ƒ (x) dx sau F = ∫ƒ dx

sunt funcții de

x

, iar

F este diferențiabil. În forma de mai sus, se numește integrale Reimann, iar funcția rezultantă însoțește o constantă arbitrară. Un integrator indefinit produce deseori o familie de funcții; prin urmare, integrala este indefinita. Integralele și procesul de integrare se află în centrul rezolvării ecuațiilor diferențiale. Cu toate acestea, spre deosebire de etapele de diferențiere, etapele de integrare nu au întotdeauna o rutină clară și standard. Ocazional, vedem că soluția nu poate fi exprimată explicit în termeni de funcție elementară. În acest caz, soluția analitică este adesea dată sub forma unui integral nedefinit. Teorema fundamentală a calculului Integralul definitiv și nedeterminat sunt legate de teorema fundamentală a calculului după cum urmează: Pentru a calcula un integral , găsiți integral

> (cunoscută și ca anti-derivată) a funcției și evaluată la punctele finale

x = a

și

x = b . Diferența dintre integrale definite și nedefinite va fi evidentă odată ce vom evalua integralele pentru aceeași funcție. Luați în considerare următorul integral: OK. Să le facem pe amândoi și să vedem diferența. Pentru integrare, trebuie să adăugăm unul la index care ne conduce la următoarea expresie: În acest moment C este doar o constantă pentru noi. Sunt necesare informații suplimentare pentru a determina valoarea exactă a

C

Să evaluăm același integral în forma sa definită i. e., cu limitele superioare și inferioare incluse.

Din punct de vedere grafic, calculăm acum suprafața sub curba

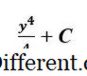
f (x) = y 3 între y = 2 și

y = 3 >.

Primul pas în această evaluare este același cu evaluarea integrală nedeterminată. Singura diferență este că de această dată nu adăugăm constant C . Expresia în acest caz arată după cum urmează: Acest lucru duce la: În esență, am înlocuit 3 și apoi 2 în expresie și am obținut diferența între ele. Aceasta este valoarea definită, spre deosebire de utilizarea C

constantă mai devreme. Să explorăm în detaliu un factor constant (cu privire la integritatea nedeterminată). Dacă y

3

este

3y

2 , atunci ∫

3y

2 dy = y ³ Cu toate acestea, 3y ² ar putea fi diferența dintre mai multe expresii dintre care unele includ

y 3 ^-5 > y ³

+7 , etc … Aceasta implică faptul că inversarea nu este unică deoarece constanta nu este înregistrată în timpul operației. ^{Deci, în general,} 3y 2 ^{este diferența dintre} y 3 + C ^unde C De altfel, C este cunoscut ca

"constantă de integrare" . ^{Se scrie astfel:} ∫ 3y ² . dx = y 3 + C Tehnicile de integrare pentru un integrat indefinit, cum ar fi căutarea de tabele sau integrarea Risch, pot adăuga noi discontinuități în timpul procesului de integrare. Aceste noi discontinuități apar deoarece anti-derivații pot necesita introducerea logaritmilor complexe. Logaritmele complexe au o discontinuitate de salt atunci când argumentul traversează axa reală negativă, iar algoritmii de integrare uneori nu pot găsi o reprezentare în cazul în care aceste sare anulează.

Dacă integritatea definită este evaluată prin calcularea mai întâi a unui integral nedefinit și apoi înlocuirea limitelor de integrare în rezultatul, trebuie să fim conștienți de faptul că integrarea pe termen nedefinită poate produce discontinuități. În plus, trebuie să investigăm discontinuitățile din intervalul de integrare.